Warning: this page is an excerpt of the book Quantum Cryptography and Secret-Key Distillation, © Cambridge University Press
Note: this page is available in XHTML+MathML, HTML only (approximate equation layout) and PDF formats.
1 Introduction
In the history of cryptography, quantum cryptography is a new and important chapter. It is a recent technique that can be used to ensure the confidentiality of information transmitted between two parties, usually called Alice and Bob, by exploiting the counterintuitive behavior of elementary particles such as photons.
The physics of elementary particles is governed by the laws of quantum mechanics, which were discovered in the early twentieth century by talented physicists. Quantum mechanics fundamentally change the way we must see our world. At atomic scales, elementary particles do not have a precise location or speed, as we would intuitively expect. An observer who would want to get information on the particle's location would destroy information on its speed – and vice versa – as captured by the famous Heisenberg uncertainty principle. This is not a limitation due to the observer's technology but rather a fundamental limitation that no one can ever overcome.
The uncertainty principle has long been considered as an inconvenient limitation, until recently, when positive applications were found.
In the meantime, the mid-twentieth century was marked by the creation of a new discipline called information theory. Information theory is aimed at defining the concept of information and mathematically describing tasks such as communication, coding and encryption. Pioneered by famous scientists like Turing and von Neumann and formally laid down by Shannon, it answers two fundamental questions: what is the fundamental limit of data compression, and what is the highest possible transmission rate over a communication channel?
Shannon was also interested in cryptography and in the way we can transmit confidential information. He proved that a perfectly secure cipher would need a secret key that is as long as the message to encrypt. But he does not say how to obtain such a long secret key. This is rather limiting because the secret key needs to be transmitted confidentially, e.g., using a diplomatic suitcase. If we had a way, say a private line, to transmit it securely, we could directly use this private line to transmit our confidential information.
Since the seventies and up to today, cryptographers have found several clever ways to send confidential information using encryption. In particular, classical ciphers encrypt messages using a small secret key, much smaller than the message size. This makes confidentiality achievable in practice. Yet, we know from Shannon's theory that the security of such schemes cannot be perfect.
Leaving aside the problem of sending confidential information, let us come back to information theory. Shannon defined information as a mathematical concept. Nevertheless, a piece of information must somehow be stored or written on a medium and, hence, must follow the laws of physics. Landauer was one of the first to realize the consequences of the fact that any piece of information ultimately exists because of its physical support. Shannon's theory essentially assumes a classical physical support. When the medium is of atomic scale, the carried information behaves quite differently, and all the features specific to quantum mechanics must be translated into an information-theoretic language, giving rise to quantum information theory.
The first application of quantum information theory was found by Wiesner in the late sixties [186]. He proposed using the spin of particles to make unforgeable bank notes. Roughly speaking, the spin of a particle obeys the uncertainty principle: an observer cannot get all the information about the spin of a single particle; he would irreversibly destroy some part of the information when acquiring another part. By encoding identification information on bank notes in a clever way using elementary particles, a bank can verify their authenticity by later checking the consistency of this identification information. At the atomic scale, the forger cannot perfectly copy quantum information stored in the elementary particles; instead, he will unavoidably make mistakes. Simply stated, copying the bank note identification information is subject to the uncertainty principle, and thus a forgery will be distinguishable from a legitimate bank note.
Other applications of quantum information theory were found. For instance, a quantum computer, that is, a computer that uses quantum principles instead of the usual classical principles, can solve some problems much faster than the traditional computer. In a classical computer, every computation is a combination of zeroes and ones (i.e., bits). At a given time, a bit can either be zero or one. In contrast, a qubit, the quantum equivalent of a bit, can be a zero and a one at the same time. In a sense, processing qubits is like processing several combinations of zeroes and ones simultaneously, and the increased speed of quantum computing comes from exploiting this parallelism. Unfortunately, the current technologies are still far away from making this possible in practice.
Following the tracks of Weisner's idea, Bennett and Brassard proposed in 1984 a protocol to distribute secret keys using the principles of quantum mechanics called quantum cryptography or more precisely quantum key distribution [10]. By again exploiting the counterintuitive properties of quantum mechanics, they developed a way to exchange a secret key whose secrecy is guaranteed by the laws of physics. Following the uncertainty principle, an eavesdropper cannot know everything about a photon that carries a key bit and will destroy a part of the information. Hence, eavesdropping causes errors on the transmission line, which can be detected by Alice and Bob.
Quantum key distribution is not only based on the principles of quantum physics, it also relies on classical information theory. The distributed key must be both common and secret. First, the transmission errors must be corrected, whether they are caused by eavesdropping or by imperfections in the setup. Second, a potential eavesdropper must know nothing about the key. To achieve these two goals, techniques from classical information theory, collectively denoted as secret-key distillation, must be used.
Unlike the quantum computer, quantum key distribution is achievable using current technologies, such as commercially available lasers and fiber optics. Furthermore, Shannon's condition on the secret key length no longer poses any problem, as one can use quantum key distribution to obtain a long secret key and then use it classically to encrypt a message of the same length. The uncertainty principle finds a positive application by removing the difficulty of confidentially transmitting long keys.
State-of-the-art ciphers, if correctly used, are unbreakable according to today's knowledge. Unfortunately, their small key size does not offer any long-term guarantee. No one knows what the future will bring, so if clever advances in computer science or mathematics once jeopardize today's ciphers' security, quantum key distribution may offer a beautiful alternative solution. Remarkably, the security of quantum key distribution is guaranteed by the laws of quantum mechanics.
Furthermore, quantum key distribution guarantees long-term secrecy of confidential data transmission. Long-term secrets encrypted today using classical ciphers could very well become illegitimately decryptable in the next decades. There is nothing that prevents an eavesdropper from intercepting an encrypted classical transmission and keeping it until technology makes it feasible to break the encryption. On the other hand, the key obtained using quantum key distribution cannot be copied. Attacking the key means attacking the quantum transmission today, which can only be done using today's technology.
For some authors, quantum cryptography and quantum key distribution are synonymous. For others, however, quantum cryptography also includes other applications of quantum mechanics related to cryptography, such as quantum secret sharing. A large portion of these other applications requires a quantum computer, and so cannot be used in practice. On the other hand, the notion of key is so central to cryptography that quantum key distribution plays a privileged role. Owing to this last comment, we will follow the first convention and restrict ourselves to quantum key distribution in the scope of this book.
1.1 A first tour of quantum key distribution
As already mentioned, quantum key distribution (QKD) is a technique that allows two parties, conventionally called Alice and Bob, to share a common secret key for cryptographic purposes. In this section, I wish to give a general idea of what QKD is and the techniques it involves. The concepts will be covered in more details in the subsequent chapters.
To ensure the confidentiality of communications, Alice and Bob agree on a common, yet secret, piece of information called a key. Encryption is performed by combining the message with the key in such a way that the result is incomprehensible by an observer who does not know the key. The recipient of the message uses his copy of the key to decrypt the message.
Let us insist that it is not the purpose of QKD to encrypt data. Instead, the goal of QKD is to guarantee the secrecy of a distributed key. In turn, the legitimate parties may use this key for encryption. The confidentiality of the transmitted data is then ensured by a chain with two links: the quantum-distributed key and the encryption algorithm. If one of these two links is broken, the whole chain is compromised; hence we have to look at the strengths of both links.
First, how is the confidentiality of the key ensured? The laws of quantum mechanics have strange properties, with the nice consequence of making the eavesdropping detectable. If an eavesdropper, conventionally called Eve, tries to determine the key, she will be detected. The legitimate parties will then discard the key, while no confidential information has been transmitted yet. If, on the other hand, no tapping is detected, the secrecy of the distributed key is guaranteed.
As the second link of the chain, the encryption algorithm must also have strong properties. As explained above, the confidentiality of data is absolutely guaranteed if the encryption key is as long as the message to transmit and is not reused for subsequent messages. This is where quantum key distribution is particularly useful, as it can distribute long keys as often as needed by Alice and Bob.
Let us detail further how QKD works. Quantum key distribution requires a transmission channel on which quantum carriers are transmitted from Alice to Bob. In theory, any particle obeying the laws of quantum mechanics can be used. In practice, however, the quantum carriers are usually photons, the elementary particle of light, while the channel may be an optical fiber (e.g., for telecommunication networks) or the open air (e.g., for satellite communications).
In the quantum carriers, Alice encodes random pieces of information that will make up the key. These pieces of information may be, for instance, random bits or Gaussian-distributed random numbers, but for simplicity of the current discussion, let us restrict ourselves to the case of Alice encoding only zeroes and ones. Note that what Alice sends to Bob does not have to – and may not – be meaningful. The whole point is that an eavesdropper cannot predict any of the transmitted bits. In particular, she may not use fixed patterns or pseudo-randomly generated bits, but instead is required to use “truly random” bits – the meaning of “truly random” in this scope will be discussed in Chapter 5.
During the tranmission between Alice and Bob, Eve might listen to the quantum channel and therefore spy on potential secret key bits. This does not pose a fundamental problem to the legitimate parties, as the eavesdropping is detectable by way of transmission errors. Furthermore, the secret-key distillation techniques allow Alice and Bob to recover from such errors and create a secret key out of the bits that are unknown to Eve.
After the transmission, Alice and Bob can compare a fraction of the exchanged key to see if there are any transmission errors caused by eavesdropping. For this process, QKD requires the use of a public classical authenticated channel, as depicted in Fig. 1.1. This classical channel has two important characteristics, namely, publicness and authentication. It is not required to be public, but if Alice and Bob had access to a private channel, they would not need to encrypt messages; hence the channel is assumed to be public. As an important consequence, any message exchanged by Alice and Bob on this channel may be known to Eve. The authentication feature is necessary so that Alice and Bob can make sure that they are talking to each other. We may think that Alice and Bob know each other and will not get fooled if Eve pretends to be either of them – we will come back on this aspect in Section 5.1.1.
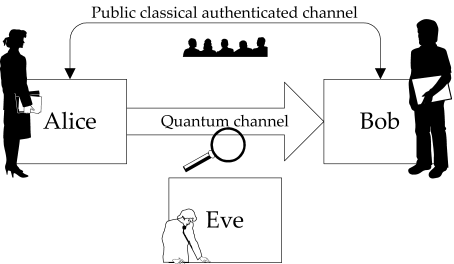
Figure 1.1: Quantum key distribution comprises a quantum channel and a public classical authenticated channel. As a universal convention in quantum cryptography, Alice sends quantum states to Bob through a quantum channel. Eve is suspected of eavesdropping on the line.
I now propose to overview the first QKD protocol, created by Bennett and Brassard in 1984, called BB84 for short [10]. More than twenty years later, BB84 can still be considered as a model for many other protocols and allows me to introduce the main concepts of QKD.
1.1.1 Encoding random bits using qubits
Any message can, at some point, be converted into zeroes and ones. In classical information theory, the unit of information is therefore the bit, that is, the set {0,1}. The quantum carriers of BB84, however, cannot be described in classical terms, so we have to adapt our language to this new setting.
There is a correspondence between the quantum state of some physical system and the information it carries. Quantum states are usually written using Dirac's notation, that is, with a symbol enclosed between a vertical bar and an angle bracket, as in |ψ〉, |1〉 or |x〉; quantum pieces of information follow the same notation.
In quantum information theory, the unit of information is the qubit, the quantum equivalent of a bit. Examples of physical systems corresponding to a qubit are the spin of an electron or the polarization of a photon. More precisely, a qubit is described by two complex numbers and belongs to the set
| {α|0〉+β|1〉:|α|2+|β|2=1,α,β∈C}, | (1.1) |
In BB84, Alice encodes random (classical) bits, called key elements, using a set of four different qubits. The bit 0 can be encoded with either |0〉 or |+〉=2-1/2|0〉+2-1/2|1〉. The bit 1 can be encoded with either |1〉 or |-〉=2-1/2|0〉-2-1/2|1〉 – note the difference in sign. In both cases, Alice chooses either encoding rule at random equally likely. Then, she sends a photon carrying the chosen qubit to Bob.
When the photon arrives at Bob's station, he would like to decode what Alice sent. For this, he needs to perform a measurement. However, the laws of quantum mechanics prohibit Bob from determining the qubit completely. In particular, it is impossible to determine accurately the coefficients α and β of the received qubit α|0〉+β|1〉. Instead, Bob must choose a pair of orthogonal qubits and perform a measurement that distinguishes only among them. We say that two qubits, |φ〉=α|0〉+β|1〉 and |ψ〉=α′|0〉+β′|1〉, are orthogonal iff αα′*+ββ′*=0.
Let us take for instance the qubits |0〉 and |1〉, which are orthogonal. So, Bob can make a measurement that distinguishes whether Alice sends |0〉 or |1〉. But what happens if she sends |+〉 or |-〉? Actually, Bob will obtain a result at random! More generally, if Bob receives |φ〉=α|0〉+β|1〉 he will measure |0〉 with probability |α|2 and |1〉 with probability |β|2 – remember that |α|2+|β|2=1. In the particular case of |+〉 and |-〉, Bob will get either |0〉 or |1〉, each with probability 1/2. Consequently, Bob is not able to distinguish between |+〉 and |-〉 in this case and gets a bit value uncorrelated from what Alice sent.
So, what is so special about the qubits |0〉 and |1〉? Nothing! Bob can as well try to distinguish any pair of orthogonal states, for instance |+〉 and |-〉. Note that |0〉 and |1〉 can be equivalently written as |0〉=2-1/2|+〉+2-1/2|-〉 and |1〉=2-1/2|+〉-2-1/2|-〉. Hence, in this case, Bob will perfectly decode Alice's key element when she sends |+〉 and |-〉, but he will not be able to distinguish |0〉 and |1〉. An example of transmission is depicted in Fig. 1.2.
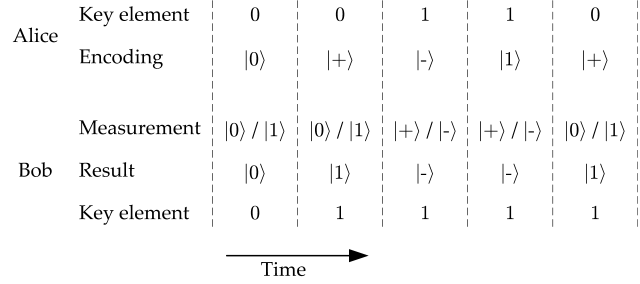
Figure 1.2: Example of transmission using BB84. The first two rows show what Alice sends. The bottom rows show the measurement chosen by Bob and a possible result of this measurement.
In the BB84 protocol, Bob randomly chooses to do either measurement. About half of the time, he chooses to distinguish |0〉 and |1〉; the rest of the time, he distinguishes |+〉 and |-〉. At this point, Alice does not reveal which encoding rule she used. Therefore, Bob measures correctly only half of the bits Alice sent him, not knowing which ones are wrong. After sending a long stream of key elements, however, Alice tells Bob which encoding rule she chose for each key element, and Bob is then able to discard all the wrong measurements; this part of the protocol is called the sifting, which is illustrated in Fig. 1.3.
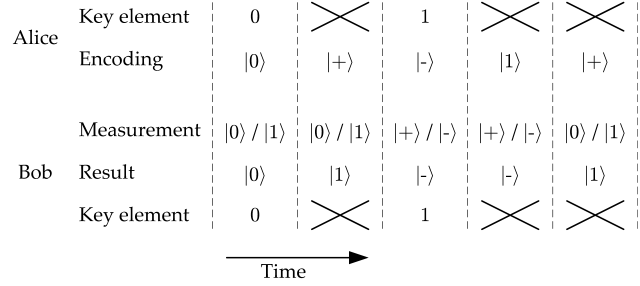
Figure 1.3: Sifting of the transmission of Fig. 1.2. The key elements for which Bob's measurement does not match Alice's encoding rule are discarded.
To summarize so far, I have described a way for Alice to send random bits to Bob. Alice chooses among four different qubits for the encoding (two possible qubits per bit value), while Bob chooses between two possible measurement procedures for the decoding. Bob is not always able to determine what Alice sent, but after sifting, Alice and Bob keep a subset of bits for which the transmission was successful. This transmission scheme allows Alice and Bob to detect eavesdropping, and this aspect is described next.
1.1.2 Detecting eavesdropping
The key feature for detecting eavesdropping is that the information is encoded in non-orthogonal qubits. Eve can, of course, intercept the quantum carriers and try to measure them. However, like Bob, she does not know in advance which set of carriers Alice chose for each key element. Like Bob, she may unsuccessfully distinguish between |0〉 and |1〉 when Alice encodes a bit as |+〉 or |-〉, or vice versa.
In quantum mechanics, measurement is destructive. Once measured, the particle takes the result of the measurement as a state. More precisely, assume that an observer measures a qubit |φ〉 so as to distinguish between |0〉 and |1〉. After the measurement, the qubit will become either |φ〉→|φ′〉=|0〉 or |φ〉→|φ′〉=|1〉, depending on the measurement result, no matter what |φ〉 was! In general, the qubit after measurement |φ′〉 is not equal to the qubit before measurement |φ〉, except if the qubit is one of those that the observer wants to distinguish (i.e., |0〉 or |1〉 in this example).
Every time Eve intercepts a photon, measures it and sends it to Bob, she has a probability 1/4 of introducing an error between Alice's and Bob's bits. Let us break this down. Eve has a probability 1/2 of measuring in the right set. When she does, she does not disturb the state and goes unnoticed. But she is not always lucky. When she measures in the wrong set, however, she sends the wrong state to Bob (e.g., |+〉 or |-〉 instead of |0〉 or |1〉). This situation is depicted in Fig. 1.4. With the wrong state, Bob will basically measure a random bit, which has a probability 1/2 of matching Alice's bit and a probability 1/2 of being wrong.
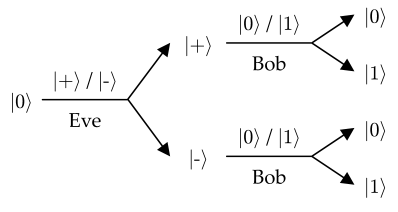
Figure 1.4: Possible events when Eve uses the wrong measurement for eavesdropping.
So, when Eve tries to eavesdrop, she will get irrelevant results about half of the time and disturb the state. She might decide not to send Bob the states for which she gets irrelevant results, but it is impossible for her to make such a distinction, as she does not know in advance which encoding is used. Discarding a key element is useless for Eve since this sample will not be used by Alice and Bob to make the key. However, if she does retransmit the state (even though it is wrong half of the time), Alice and Bob will detect her presence by an unusually high number of errors between their key elements.
Both Bob and Eve have the same difficulties in determining what Alice sent, since they do not know which encoding is used. But the situation is not symmetric in Bob and Eve: all the communications required to do the sifting are made over the classical authenticated channel. This allows Alice to make sure she is talking to Bob and not to Eve. So, the legitimate parties can guarantee that the sifting process is not influenced by Eve. Owing to this, Alice and Bob can select only the key elements which are correctly measured.
To detect the presence of an eavesdropper, Alice and Bob must be able to detect transmission errors. For this, an option is to disclose a part of the sifted key. A given protocol might specify that after a transmission of l+n key elements (e.g., l+n=100 000), numbered from 0 to l+n-1, Alice randomly chooses n indexes (e.g., n=1000) and communicates them to Bob. Alice and Bob then reveal the corresponding n key elements to one another so as to count the number of errors. Any error means there was some eavesdropping. The absence of error gives some statistical confidence on the fact that there was no eavesdropping – Eve might just have been lucky, guessing right the encoding sets or making errors only on the other l key elements. Of course, only the remaining l key elements will then be used to produce a secret key.
1.1.3 Distilling a secret key
In the case where errors are detected, Alice and Bob may decide to abort the protocol, as errors may be caused by eavesdropping. At least, this prevents the creation of a key that can be known to the adversary. This kind of decision, however, may be a little stringent. In practice, the physical implementation is not perfect and errors may occur for many reasons other than eavesdropping, such as noise or losses in the quantum channel, imperfect generation of quantum states or imperfect detectors. Also, Eve may just eavesdrop a small fraction of the sifted key, making the remaining key elements available for creating a secret key. There should thus be a way to make a QKD protocol more robust against noise.
Alice and Bob count the number of errors in the disclosed key elements and divide this number by n to obtain an estimate of the expected fraction e of transmission errors in the whole set of key elements; e is called the bit error rate. They can then deduce the amount of information Eve knows about the key elements. For instance, they can statistically estimate that Eve knows no more than, say, IE bits on the l key elements. This is the estimation part of the protocol. The formula giving the quantity IE is not described here; it results from an analysis of what an eavesdropper may do given the laws of quantum mechanics. Also, the quantity IE does not precisely tell Alice and Bob what Eve knows about the key elements. She may know the exact value of IE key elements or merely the result of some arbitrary function of the l key elements, which gives her IE bits of information in the Shannon sense.
At this point, Alice and Bob know that the l undisclosed key elements have some error rate e and that a potential eavesdropper acquired up to IE bits of information on them. Using the public classical authenticated channel, Alice and Bob can still try to make a fully secret key; this part is called secret-key distillation.
Secret-key distillation usually comprises a step called reconciliation, whose purpose is to correct the transmission errors, and a step called privacy amplification, which wipes out Eve's information at the cost of a reduced key length. I shall briefly describe these two processes.
In the case of BB84, the reconciliation usually takes the form of an interactive error correction protocol. Alice and Bob alternatively disclose parities of subsets of their key elements. When they encounter a diverging parity, it means that there is an odd number of errors in the corresponding subset, hence at least one. Using a dichotomy, they can narrow down the error location and correct it. They repeat this process a sufficient number of times and the result is that Alice and Bob now share equal bits.
For secret-key distillation, all the communications are made over the public authenticated classical channel. Remember that Eve cannot intervene in the process but she may listen to exchanged messages, which in this case contain the exchanged parity bits. Therefore, the knowledge of Eve is now composed of IE+|M| bits, with |M| the number of parity bits disclosed during the reconciliation.
To make the key secret, the idea behind privacy amplification is to exploit what Eve does not know about the key. Alice and Bob can calculate a function f of their key elements so as to spread Eve's partial ignorance over the entire result. Such a function (e.g., like a hashing function in classical cryptography) is chosen so that each of its output bits depends on most of, if not all, the input bits. An example of such a function consists of calculating the parity of random subsets of bits. Assume, for instance, that Eve perfectly knows the bit x1 but does not know anything about the value of the bit x2. If the function f outputs x1+x2mod2, Eve has no clue on this output value since the two possibilities x1+x2=0(mod2) and x1+x2=1(mod2) are equally likely no matter what the value of x1 is.
The price to pay for privacy amplification to work is that the output (secret) key must be smaller than the input (partially secret) key. The reduction in size is roughly equal to the number of bits known to Eve, and the resulting key size is thus l-IE-|M| bits. To maximize the key length and perhaps to avoid Eve knowing everything about the key (e.g., l-IE-|M|=0), it is important that the reconciliation discloses as little information as possible, just enough to make Alice and Bob able to correct all their errors.
Notice that errors on the quantum transmission are paid twice, roughly speaking, on the amount of produced secret key bits. First, errors should be attributed to eavesdropping and are counted towards IE. Second, errors must be corrected, for which parity bits must be publicly disclosed and are counted towards |M|.
Finally, the secret key obtained after privacy amplification can be used by Alice and Bob for cryptographic purposes. In particular, they can use it to encrypt messages and thus create a secret channel.
1.1.4 Further reading
For more information, I would like to point out the paper by Bennett, Brassard and Ekert [12]. One can also find more technical information in the review paper by Gisin, Ribordy, Tittel and Zbinden [64].
1.2 Notation and conventions
Throughout this book, we use random variables. A discrete random variable X is a pair composed of a finite set X and a probability distribution on X. The elements x of X are called symbols. The probability distribution is denoted as PX(x)=Pr[X=x] for x∈X and of course verifies the relations PX(x)≥0 and ∑xPX(x)=1. We will use capital roman letters for random variables, the corresponding lower-case roman letters for the particular values (or symbols) that they can take, and the corresponding capital script letter for the sets over which they are defined.
The continuous random variables are defined similarly. A continuous random variable X is defined as an uncountable set X together with a probability density function pX(x) on X.
The other important definitions are given along the way. For a list of the main symbols and abbreviations, please refer to the Appendix.