Avril 2002
1 Université Libre de Bruxelles, service Théorie de l'Information et des Communications (Prof. N. Cerf).
2 Proton World, member of ERG Group, Smart Card Security Center of Excellence (Y. Moulart).
Dernier cri en matière de haute technologie, la cryptographie quantique garantit une confidentialité absolue de l'information échangée au sein d'une fibre optique. Le secret de cette prouesse tient à la possibilité de véhiculer l'information par l'intermédiaire du constituant élémentaire de la lumière: le photon.
Comment communiquer des messages secrets et s'assurer qu'ils ne seront pas compris par une indésirable tierce personne? La cryptographie est la discipline qui essaie de répondre à cette question.
Dans la cryptographie traditionnelle, seul le code de Vernam permet d'établir un canal inconditionnellement sûr entre un émetteur (Alice) et un récepteur (Bob). Ce code demande à Alice et Bob de se mettre d'accord sur une clé secrète prédéterminée. Alice chiffre le message grâce à cette clé, et le message chiffré ne peut être ensuite déchiffré que moyennant cette même clé, donc par Bob. La règle de chiffrement est simple. Supposons qu'Alice veuille transmettre un bit d'information. Pour cela, elle utilise un bit de la clé avec lequel elle effectue une opération de "ou-exclusif" avec le bit à transmettre. Bob peut ainsi refaire cette même opération de son côté, annulant ainsi le premier "ou-exclusif", pour déchiffrer le bit transmis.
Malheureusement, le code de Vernam présente un inconvénient majeur. Pour que la méthode reste inviolable, la clé doit consister en autant de bits secrets qu'il y a de bits d'information à transmettre car la clé secrète ne peut être utilisée qu'une seule fois. Une clé utilisée plus d'une fois fait perdre au code de Vernam ses propriétés d'inviolabilité et a permis, notamment durant la seconde guerre mondiale, aux Allemands de décoder l'information secrète lors de transmissions successives.
Strictement parlant, la clé secrète doit être préalablement échangée de main à main par Alice et Bob. Cela signifie que si l'on veut transmettre un Gigabit d'information secrète, Alice et Bob devront se rencontrer pour échanger, par exemple, un CD-Rom contenant un milliard de bits aléatoires. Cette procédure, quoique sûre, n'est pas réaliste à l'usage car elle impose à Alice et à Bob de devoir se rencontrer même s'ils veulent ensuite communiquer à une distance de 10 000 km.
Aussi, les mathématiciens ont développé d'autres méthodes de cryptographie visant à remédier à ces difficultés.
La première différence entre le code de Vernam et les méthodes de chiffrement actuelles consiste à remplacer la simple opération de "ou-exclusif" par une opération beaucoup plus compliquée entre la clé et le message en clair. De cette manière, il est pratiquement infaisable de retrouver le message en clair à partir du message chiffré, ou même, de retrouver la clé à partir d'un message en clair et du message chiffré correspondant, et cela même si la clé est beaucoup plus petite que le message à envoyer. C'est le cas, par exemple, de l'algorithme de chiffrement par bloc DES [4] ou du plus récent algorithme belge Rijndael, choisi pour devenir le nouveau standard AES [5].
Grâce à ces algorithmes, Alice et Bob peuvent maintenant échanger une clé de petite taille valable pour chiffrer des messages de grande taille. Le prix à payer pour arriver à cela est la perte de la sécurité absolue par l'ajout d'une hypothèse. En théorie, il est maintenant possible de retrouver le message en clair à partir du message chiffré, mais cela est suffisamment difficile à faire pour supposer que l'ennemi n'a pas les ressources de calcul suffisantes pour y arriver.
En pratique, cette hypothèse est tout à fait réaliste. Un hacker aura en général beaucoup plus de facilités à percer les failles d'un système informatique qu'à se lancer dans les calculs nécessaires à casser l'algorithme, même en possession du plus puissant des ordinateurs. Cependant, rien ne dit que, à long terme, les développements des mathématiques ou de l'informatique ne rendent pratiquement faisable l'extraction du message en clair à partir du message chiffré.
La seconde amélioration apportée par la cryptographie moderne est l'introduction de la cryptographie à clé publique, permettant à Alice et Bob de ne pas devoir se rencontrer préalablement à la transmission de messages secrets pour échanger la clé.
Dans les systèmes à clé publique, couramment utilisés de nos jours, chaque correspondant possède deux clés. Une des clés est publique et donc connue de tous (par exemple, publiée dans un répertoire), et elle ne permet que de chiffrer un message, pas de le déchiffrer. Au contraire, la seconde clé est privée et ne permet que le déchiffrage. Pour envoyer un message d'Alice à Bob, la procédure est la suivante. Si cela n'est pas encore fait, Alice se procure la clé publique de Bob (via une base de donnée publique ou elle la demande simplement à Bob). Ensuite, Alice utilise la clé publique de Bob pour chiffrer son message confidentiel et envoie l'information chiffrée à Bob. Ce dernier est la seule personne en possession de la clé privée correspondante et donc la seule personne capable de déchiffrer le message qu'Alice vient de lui envoyer. Dans ce schéma, l'idée essentielle est que le chiffrement est public au sens où n'importe qui peut envoyer un message chiffré à Bob, mais le déchiffrement nécessite la connaissance de la clé privée.
De nouveau, les avantages pratiques de la cryptographie à clé publique sont à comparer à la perte relative de sécurité qu'elle introduit. Un lien existe entre une clé publique et sa clé privée correspondante et il est donc en théorie possible de retrouver l'une à partir de l'autre. Cependant, il est heureusement très difficile d'effectuer cette opération dans le cadre des connaissances actuelles et de la puissance des ordinateurs d'aujourd'hui.
Pour fixer les idées, prenons l'exemple de l'algorithme Rivest-Shamir-Adleman (RSA) qui peut être utilisé à la base d'un système de chiffrement à clé publique [4]. Dans ce système, le lien entre la clé publique et privée se trouve si l'on est capable de factoriser des nombres de plusieurs centaines de chiffres, ce qui est très difficile actuellement. En effet, alors qu'il est facile de multiplier deux grands nombres premiers, les retrouver à partir du produit l'est beaucoup moins. Malheureusement, les progrès dans la factorisation mettent toujours la barre plus haute pour les cryptographes qui doivent se baser sur des tailles de clés, et donc des nombres à factoriser, de plus en plus grandes. De plus, si un mathématicien découvre un jour un algorithme permettant de factoriser rapidement des grands nombres, il pourra déchiffrer tous les messages chiffrés avec RSA sans que personne ne s'en aperçoive, puisqu'il a accès à toutes les clés publiques.
Cette menace est d'autant plus forte que les physiciens ont imaginé une nouvelle manière de faire des calculs grâce à l'ordinateur quantique. Cette nouvelle génération d'ordinateurs, encore à un stade essentiellement théorique, a la propriété de pouvoir résoudre rapidement certains problèmes réputés difficiles avec les techniques informatiques traditionnelles. Ainsi, Peter Shor [6] a découvert un algorithme quantique (c'est-à-dire tournant sur un ordinateur quantique) permettant la factorisation de grands nombres dans des délais raisonnables.
Il semble donc que beaucoup de menaces pèsent sur la sécurité à long terme des techniques cryptographiques actuelles. Ainsi par exemple, la cryptographie à clé publique, quoique populaire et offrant encore un niveau de sécurité largement suffisant, ne donne aucune garantie à long terme quant à la confidentialité des données qu'elle doit protéger. C'est pourquoi nous voulons présenter ici une manière alternative de gérer la confidentialité d'un message, sans faire d'hypothèse technologique ou de complexité, c'est-à-dire sur la rapidité pratique de telle ou telle opération mathématique avec les ordinateurs d'aujourd'hui.
Sommes-nous donc condamnés à échanger des mégabits de clés secrètes prédéterminées de main à main pour garantir la confidentialité la plus absolue? Au regard des lois de la physique les plus fondamentales connues à ce jour, ce n'est pas certain. La physique quantique, décrivant la dynamique intime de chaque particule élémentaire (photons, atomes, ...) constituant notre univers, pourrait pallier à cette difficulté et permettre de construire des protocoles de communication sans aucune faille pour la sécurité. C'est tout l'objet de la cryptographie quantique.
La cryptographie quantique a vu son apparition voici une quinzaine d'année quand deux chercheurs, Charles Bennett et Gilles Brassard [1], ont eu l'idée d'utiliser les principes de la physique quantique pour transmettre des messages de façon confidentielle. La transmission se fait au moyen d'impulsions de photon individuel (« quanta » de lumière) envoyées d'un émetteur (Alice) à un récepteur (Bob) et voyageant à travers une fibre optique.
C'est le théorème dit de « non-clonage » qui empêche, en physique quantique, qu'une troisième partie (Eve) puisse décoder l'information transmise. On démontre en effet qu'à moins que l'on ait une caractérisation précise et connue d'avance de l'état quantique décrivant la lumière et en particulier de l'état du photon, il nous est impossible de reproduire cet état, c'est-à-dire d'en faire un clone. Autrement dit, le simple fait de vouloir observer tout photon pour le caractériser le dénature complètement sans que, par après, on puisse le remettre dans son état initial ou encore en produire un clone. Ce théorème de « non-clonage » s'avère être une mauvaise nouvelle pour toute tentative de caractériser complètement l'état quantique d'un photon. En revanche, il peut être reconsidéré de façon positive dans le domaine de la cryptographie. En effet, Eve, qui désire collecter l'information secrète sans être vue, devra nécessairement copier au préalable l'état quantique du photon. Comme cela lui est impossible, elle devra au mieux deviner l'état dans lequel le photon se trouve. En procédant ainsi, elle introduit des modifications qui dénaturent le photon et devient ainsi vulnérable à toute détection ultérieure d'Alice ou de Bob.
Le but essentiel est donc de permettre à Alice et Bob d'échanger une clé secrète avec l'assurance que toute écoute de la part d'une tierce personne pourra être détectée. Si cette clé secrète a été correctement transmise, Alice et Bob peuvent l'utiliser en combinaison avec le code de Vernam décrit plus haut, afin d'obtenir un système cryptographique inconditionnellement sûr et ce, même à distance.
Partant de l'idée du non-clonage, les chercheurs ont élaboré un protocole de communication en utilisant la polarisation du photon pour encoder des bits pouvant constituer une clé secrète. Le photon possède en effet deux états dit de polarisation qui se distinguent notamment grâce à un filtre polariseur (comme un cristal de Calcite par exemple). Ainsi, une lumière polarisée verticalement passera à travers ce filtre orienté dans le même sens. Par contre, la lumière polarisée horizontalement ne passera pas et sera absorbée au sein du filtre. Si maintenant la lumière est polarisée diagonalement à 45°, seulement la moitié de l'intensité lumineuse passera. Qu'en est-il si nous ne laissons passer qu'un seul photon à la fois, polarisé diagonalement, à travers du filtre? Clairement le photon ne peut être divisé en deux puisqu'il est le grain indivisible de lumière. L'expérience montre, tout comme le prédit la théorie quantique, qu'il passe une fois sur deux à travers le polariseur et qu'une fois sur deux il est absorbé.

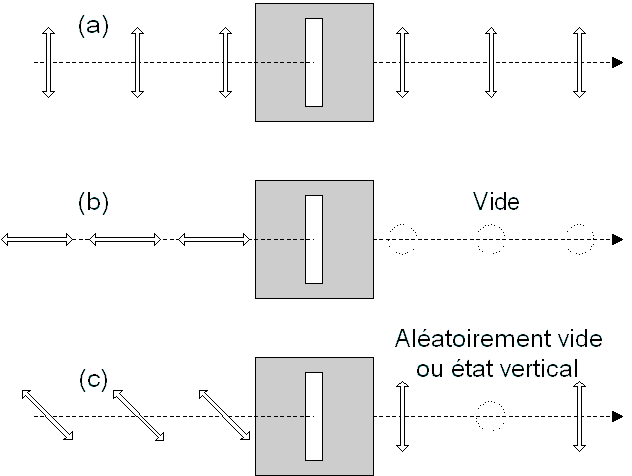
Figure 1: Photon unique traversant un filtre ne laissant passer que la lumière polarisée verticalement. (a) Les états polarisés verticalement traversent le filtre sans être absorbés. (b) Les états polarisés horizontalement sont tous absorbés. (c) Les états polarisés diagonalement sont aléatoirement absorbés ou transmis. Un observateur placé après le filtre ne pourrait donc pas, de manière déterministe, distinguer l'état du photon avant le filtre, par rapport à un état de polarisation soit verticale soit horizontale.
Si Alice se restreint à encoder des bits secrets dans les deux états de polarisation verticale et horizontale, Bob est à même de lire ces bits en distinguant la polarisation de chaque photon grâce au filtre. Mais alors Eve est à même d'intercepter la communication sans être vue. Il lui suffit de détecter ces bits de la même manière que Bob et par la suite d'encoder à nouveau les bits dans la polarisation de photons, de la même façon qu'Alice, et de les renvoyer à Bob. En revanche, Alice peut concevoir une stratégie dans laquelle l'encodage de polarisation des photons est une fois sur deux orientée verticalement et horizontalement ou une fois sur deux diagonalement à 45° et 135°. Dans ce cas, Eve devra être capable de distinguer parmi quatre états distincts de polarisation. Or, un filtre polarisant n'en distingue que deux selon des axes orthogonaux et, selon les principes de la mécanique quantique, il n'est pas possible d'en réaliser un qui isole un état parmi les quatre états de polarisation.
Cette impossibilité est une illustration de ce fameux théorème de non-clonage. Si un tel polariseur existait, alors nous pourrions caractériser l'état de polarisation du photon de façon non ambiguë et recréer autant de clones nécessaires dans le même état. Ainsi Eve pourrait garder une copie pour elle et en envoyer une autre vers Bob, tout cela sans être vue. Etant donné le théorème de non-clonage, le mieux qu'elle puisse faire est d'orienter au hasard son polariseur dans le sens vertical ou diagonal, ce qui introduit inévitablement des erreurs et perturbe la communication.
Ce qui arrive à Eve arrive aussi inévitablement à Bob qui, lui, doit se donner également l'axe dans lequel il mesure la polarisation. Pour pouvoir échanger des bits secrets dans cette situation, Bob doit alors communiquer publiquement à Alice l'axe de polarisation dans lequel il a réalisé sa mesure. Ensuite, Alice compare les axes dans lesquels elle a envoyé chaque bit avec les axes que Bob a choisi. S'ils correspondent, Alice le communique publiquement à Bob et un bit secret est ainsi échangé; sinon, le bit sera purement et simplement rejeté car aucune correspondance n'existe.
L'intervention de Eve ne peut aboutir qu'à induire en erreur Alice et Bob sur le bit secret échangé. Supposons par exemple que Eve mesure le photon dans une polarisation diagonale alors qu'Alice l'avait envoyé avec une polarisation verticale. Eve renvoie un photon à Bob dans la polarisation qu'elle a mesurée. Si par malheur Bob mesure une polarisation horizontale, bien que les axes de polarisation choisis par Alice et Bob correspondent, le bit secret échangé sera différent. Pour détecter la présence de Eve, il suffit alors dans le grand nombre de bits échangés d'en sacrifier un petit nombre. Cette fraction du nombre de bits est communiquée publiquement entre Alice et Bob pour vérifier le taux d'erreur durant la communication. Si ce taux d'erreur, qui tient aussi compte d'inévitables erreurs dues à des imperfections techniques, est anormalement élevé, cela signifie que la communication a été interceptée.
Dans ce protocole, la sécurité se fonde entre autres sur l'inexistence d'un filtre polarisant permettant de distinguer parmi quatre états. Comment donc y croire si ce n'est de faire confiance aux physiciens? La théorie quantique permet d'interpréter de la façon la plus précise qui nous est donnée à ce jour tous les phénomènes physiques connus. Elle décrit aussi bien les phénomènes microscopiques qui se passent à l'échelle des particules élémentaires et des atomes que les phénomènes macroscopiques qui découlent de la dynamique collective de ces mêmes particules et atomes. Et si le siècle d'existence de cette théorie jamais mise en défaut ne suffit pas à convaincre le lecteur, alors ne pourrait-on pas imaginer qu'un homme passe-muraille voire l'homme invisible puisse fouiller dans les informations confidentielles de l'ordinateur d'autrui? La théorie quantique ne prédit pas à ce jour ces éventualités ni même que d'autres démons malveillants puissent exister. En d'autres mots, croire à la réalité du monde qui nous entoure c'est aussi croire aux prédictions de la physique quantique.
Basés sur le même principe fondamental, de nombreux laboratoires ont pu réaliser expérimentalement des protocoles de cryptographie quantique. Un câble optique du réseau téléphonique ordinaire a permis de transporter sur 20 kilomètres, sous le lac Léman, des informations quantiques confidentielles. Sans entrer dans les détails, le dispositif utilise l'interférométrie optique plutôt que la polarisation de la lumière pour transmettre l'information. Toutefois, l'appareillage, bien que parfaitement opérationnel, présente encore quelques inconvénients. Le premier problème est que, à cause de pertes du signal dans la fibre optique, la transmission ne peut se faire que sur une relativement courte distance, limitant l'application possible pour des communications quantiques à l'intérieur d'une grande ville. Ce problème est l'objet d'une investigation théorique poussée de la part des chercheurs mais, au stade actuel, il n'est pas entièrement résolu. Le deuxième inconvénient est que le contrôle expérimental de la production d'impulsions à un photon, ainsi que sa détection, s'avèrent encore imparfaits. Un contrôle parfait de la dynamique du photon depuis sa création jusqu'à sa détection permettrait un débit plus important de bits secrets. De toute évidence, les recherches et développements dans ce domaine évoluent de façon constante et s'approchent d'une phase de commercialisation à relativement court terme.
De nombreuses autres améliorations de la cryptographie quantique sont actuellement à l'étude, entre autres à l'Université Libre de Bruxelles dans le Service Théorie de l'Information et des Communications. Plusieurs projets de recherche en cours, en collaboration avec le Service Optique et Acoustique et le Service Physique Théorique, visent à accroître le débit de bits secrets échangés ou la portée du dispositif cryptographique via l'usage d'alphabets plus que binaires. D'autres travaux théoriques en collaboration avec d'autres laboratoires européens se concentrent sur la possibilité d'employer des faisceaux de lumière intense (plusieurs photons) mais gardant les caractéristiques quantiques permettant la cryptographie quantique, et ce dans le but de contourner les défis technologiques liés à l'emploi d'un photon unique. Ce sont certains types d'états, dits "cohérents" et "comprimés", du rayonnement qui pourraient être ainsi utilisés.
Comme on peut le constater, la cryptographie quantique rassemble une multitude de disciplines. On y trouve des questions de mathématiques et de physique fondamentale très abstraites, portant sur la mécanique quantique, des questions de recherche de performances accrues sur l'instrumentation optique utilisée (laser, détecteur, fibre optique), des questions liées à l'adaptation des résultats à des fins industrielles, sans parler des questions éthiques que posent la confidentialité dans le monde d'aujourd'hui. En bref, c'est un sujet d'actualité qui recouvre un très large éventail de compétences, allant de la physique fondamentale jusqu'aux applications industrielles. Le résultat de ces recherches devrait aboutir à augmenter la sécurité de nos transmissions confidentielles, toujours plus nombreuses pour ce qui concerne le commerce en ligne et les transactions financières.
Pour en savoir plus, nous conseillons au lecteur les articles de vulgarisation [1] et [2] ou l'article, plus technique, de revue [3].
[1] C.H. Bennett, G. Brassard, A.K. Ekert, Sc. Am. 267, 50 (1992).
[2] N. Cerf, N. Gisin, La Recherche 327, 46 (2000).
[3] N.Gisin, G. Ribordy, W. Tittel, H. Zbinden, Rev. Mod. Phys. 74, 145 (2002).
[4] A. J. Menezes, P. C. van Oorschot, S. A. Vanstone, Handbook of Applied Cryptography, CRC Press (1996).
[5] J. Daemen, V. Rijmen, The block cipher Rijndael.
[6] P.W. Shor, Proceedings of the 35th Annual Symposium on the Foundations of Computer Science, 124 (1994).